Kvartikaning bitangentsalari - Bitangents of a quartic
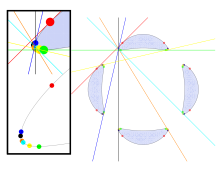
Algebraik nazariyada tekislik egri chiziqlari, general kvartik tekislik egri chizig'i 28 ga ega achchiq egri chiziqqa tegib turgan chiziqlar, chiziqlar ikki joyda. Ushbu satrlar mavjud murakkab proektsion tekislik, ammo bu barcha 28 satrga ega bo'lgan kvartik egri chiziqlarni aniqlash mumkin haqiqiy raqamlar sifatida ularning koordinatalari va shuning uchun ga tegishli Evklid samolyoti.
Yigirma sakkizta haqiqiy bitangents bilan aniq kvartikani birinchi marta bergan Pluker (1839 )[1] Pluker ko'rsatganidek, har qanday kvartikaning haqiqiy bitangentsalari soni 28, 16 yoki 9 dan kam bo'lishi kerak. Yana 28 ta haqiqiy bitangentsaga ega kvartik hosil bo'lishi mumkin. lokus markazlari ellipslar ikkita parallel bo'lmagan chiziqlarga teginadigan sobit o'q uzunliklari bilan.[2]Shioda (1995) a proektsiyalash natijasida hosil bo'lgan yigirma sakkiz bitangentsali kvartikaning boshqacha konstruktsiyasini berdi kubik sirt; Shiodaning egri chizig'idan yigirma yettitasi haqiqiy, yigirma sakkizinchisi esa cheksiz chiziq proektsion tekislikda.
Misol
The Trott egri chizig'i, 28 ta haqiqiy bitangentsaga ega bo'lgan yana bir egri chiziq, bu nuqtalar to'plamidir (x,y) qoniqarli daraja to'rt polinom tenglama
Ushbu nuqtalar o'ziga xos bo'lmagan kvartik egri chiziqni hosil qiladi tur uchta va u yigirma sakkizta haqiqiyga ega bitangents.[3]
Plyuker va Blum va Gvinand misollari singari, Trott egri chizig'i to'rtta ovalga, to'rtinchi egri chiziq uchun maksimal songa ega va shuning uchun M-egri chiziq. To'rt ovalni oltita turli xil juft ovallarga birlashtirish mumkin; har bir oval juftlik uchun juftlikdagi ikkala ovalga tegadigan to'rtta bitangens mavjud, ikkitasi ikkala ovalni ajratib turadi, ikkitasi esa yo'q. Bundan tashqari, har bir oval tekislikning qavariq bo'lmagan mintaqasini chegaralaydi va uning chegarasining qavariq bo'lmagan qismini qamrab oluvchi bitansensiga ega.
Boshqa tuzilmalarga ulanish
The ikki tomonlama egri kvartik egri chiziqqa dastlabki oddiy egri chiziqning 28 bitangentsasiga teng bo'lgan ikkita 28 oddiy oddiy juftlik mavjud.
Kvartikaning 28 bitangentsasi, shuningdek, shakl belgilari bilan yozishmalarda joylashtirilishi mumkin
qayerda a, b, v, d, e va f barchasi nol yoki bitta va qaerda
- reklama + bo'lishi + cf = 1 (mod 2).[4]
Uchun 64 ta tanlov mavjud a, b, v, d, e va f, ammo bu tanlovlarning atigi 28 tasi g'alati summani hosil qiladi. Shuningdek, kimdir izohlashi mumkin a, bva v sifatida bir hil koordinatalar ning bir nuqtasi Fano samolyoti va d, eva f xuddi shu cheklangan proektsion tekislikdagi chiziq koordinatalari sifatida; yig'indining toq bo'lishi sharti nuqta va chiziqning bir-biriga tegmasligini talab qilish bilan tengdir, va nuqta va chiziqning tegmaydigan 28 xil juftligi mavjud.
Fano tekisligining to'qnashuvsiz nuqta chiziqli juftligidan ajratilgan nuqta va chiziqlari uchburchak hosil qiladi va kvartikaning bitangentsalari Fano tekisligining 28 uchburchagi bilan yozishmalar sifatida qabul qilingan.[5] The Levi grafigi Fano samolyotining Heawood grafigi, unda Fano tekisligining uchburchagi 6 tsikl bilan ifodalanadi. Heawood grafigining 28 6 tsikli o'z navbatida ning 28 tepasiga to'g'ri keladi Kokseter grafigi.[6]
Kvartikaning 28 bitangentsasi -2 darajadagi 56 qatorning juftlariga ham to'g'ri keladi del Pezzo yuzasi,[5] va 28 toqgacha teta xususiyatlari.
Kubdagi 27 chiziq va kvartikadagi 28 bitangens, 4-turdagi kanonik sekstik egri chizig'ining 120 tritangens tekisligi bilan birgalikda "uchlik "ma'nosida Vladimir Arnold, xususan McKay yozishmalari,[7][8][9] va boshqa ko'plab ob'ektlar bilan bog'liq bo'lishi mumkin, shu jumladan E7 va E8, muhokama qilinganidek uchlik.
Izohlar
- ^ Masalan, qarang. Kulrang (1982).
- ^ Blum va Gvinand (1964).
- ^ Trott (1997).
- ^ Riman (1876); Keyli (1879).
- ^ a b Manivel (2006).
- ^ Dejter, Italo J. (2011), "Kokseter grafigidan Klein grafigigacha", Grafika nazariyasi jurnali, arXiv:1002.1960, doi:10.1002 / jgt.20597.
- ^ le Bryuyn, Liven (2008 yil 17-iyun), Arnoldning uchliklari, dan arxivlangan asl nusxasi 2011-04-11
- ^ Arnold 1997, p. 13 - Arnold, Vladimir, 1997, Toronto ma'ruzalari, 2-ma'ruza: Majoziylashtirish, komplekslashtirish va matematik uchliklar, 1997 yil iyun (so'nggi yangilangan avgust, 1998 yil). TeX, PostScript, PDF
- ^ (McKay & Sebbar 2007 yil, p. 11)
Adabiyotlar
- Blum, R .; Gvinand, A. P. (1964), "28 ta haqiqiy bitangentli kvartika", Kanada matematik byulleteni, 7: 399–404, doi:10.4153 / cmb-1964-038-6.
- Keyli, Artur (1879), "Kvartika bitangentsalari to'g'risida", Salmonning yuqori tekislik egri chiziqlari, 387-389 betlar. Yilda Artur Keylining to'plangan matematik hujjatlari, Endryu Rassel Forsit, tahr., University Press, 1896, jild. 11, 221-223 betlar.
- Kulrang, Jeremi (1982), "Oddiy guruh tarixidan", Matematik razvedka, 4 (2): 59–67, doi:10.1007 / BF03023483, JANOB 0672918. Qayta nashr etildi yilda Levi, Silvio, tahrir. (1999), Sakkizta yo'l, MSRI nashrlari, 35, Kembrij universiteti matbuoti, 115-131-betlar, ISBN 0-521-66066-1, JANOB 1722415.
- Manivel, L. (2006), "Lie algebralarining chiziqlari va modellarining konfiguratsiyasi", Algebra jurnali, 304 (1): 457–486, arXiv:matematik / 0507118, doi:10.1016 / j.jalgebra.2006.04.029.
- Pluker, J. (1839), Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie, Berlin: Adolf Markus.
- Riman, G. F. B. (1876), "Zur Theorie der Abel'schen Funktionen für den Fall p = 3", Ges. Werke, Leypsig, 456-472 betlar. Keyli keltirganidek.
- Shioda, Tetsuji (1995), "Weierstrass transformatsiyalari va kubikli yuzalar" (PDF), Matematik Universitatis Sancti Pauli sharhlari, 44 (1): 109–128, JANOB 1336422[doimiy o'lik havola ].
- Trott, Maykl (1997), "GroebnerBasis-ni geometriyadagi uchta muammoga qo'llash", Matematika Ta'lim va tadqiqot, 6 (1): 15–28.


![chap [egin {array} {ccc} a & b & c d & e & f end {array} ight]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f9c527454b1e1f26c9be9078ebac08b5492bbfc)